What is the function of a lever and Examples of a levers?

The lever is the most wonderful mechanical element in the world. The expression, lever, is not employed in the sense of a stick or a bar which is used against a fulcrum to lift or push something with, but as the type of numerous devices which employ the same principle.

Excerpt from the book: Practical Mechanics for Boys / Author: J. S. Zerbe

Some of these devices are, the wedge, the screw, the pulley and the inclined plane. In some form or other, one or more of these are used in every piece of mechanism in the world.

Because the lever enables the user to raise or move an object hundreds of times heavier than is possible without it, has led thousands of people to misunderstand its meaning, because it has the appearance, to the ignorant, of being able to manufacture power.

Wrong Inferences from Use of Lever

This lack of knowledge of first principles, has bred and is now breeding, so-called perpetual motion inventors (?) all over the civilized world. It is surprising how many men, to say nothing of boys, actually believe that power can be made without the expenditure of something which equalizes it

The boy should not be led astray in this particular, and I shall try to make the matter plain by using the simple lever to illustrate the fact that whenever power is exerted some form of energy is expended.

In Fig. 1 is a lever (A), resting on a fulcrum (B), the fulcrum being so placed that the lever is four times longer on one side than on the other. A weight (C) of 4 pounds is placed on the short end, and a 1-pound weight (D), called the power, on the short end. It will thus be seen that the lever is balanced by the two weights, or that the weight and the power are equal.

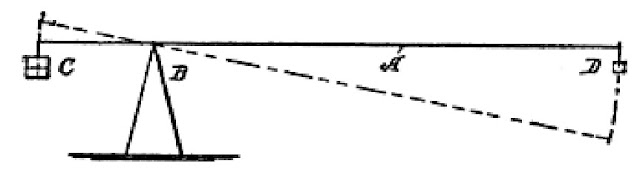Fig. 1. Simple Lever

The Lever Principle

Now, without stopping to inquire, the boy will say: "Certainly, I can understand that. As the lever is four times longer on one side of the fulcrum than on the other side, it requires only one-fourth of the weight to balance the four pounds.
But suppose I push down the lever, at the point where the weight (D) is, then, for every pound I push down I can raise four pounds at C.
In that case do I not produce four times the power?"

I answer, yes.
But while I produce that power I am losing something which is equal to the power gained.

What is that?

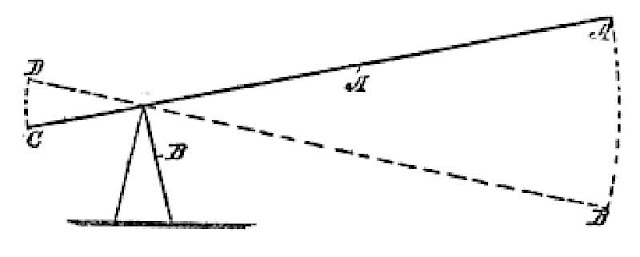Fig. 2. Lever Action

First: Look at Fig. 2; the distance traveled. The long end of the lever is at its highest point, which is A; and the short end of the lever is at its lowest point C. When the long end of the lever is pushed down, so it is at B, it moves four times farther than the short end moves upwardly, as the distance from C to D is just one-fourth that from A to B. The energy expended in moving four times the distance balances the power gained.

Power vs. Distance Traveled

From this the following law is deduced: That whatever is gained in power is lost in the distance traveled

Second: Using the same figure, supposing it was necessary to raise the short end of the lever, from C to D, in one second of time. In that case the hand pressing down the long end of the lever, would go from A to B in one second of time; or it would go four times as far as the short end, in the same time.

Power vs. Loss in Time

This means another law: That what is gained in power is lost in time.

Distinguish clearly between these two motions. In the first case the long end of the lever is moved down from A to B in four seconds, and it had to travel four times the distance that the short end moves in going from C to D.

In the second case the long end is moved down, from A to B, in one second of time, and it had to go that distance in one-fourth of the time, so that four times as much energy was expended in the same time to raise the short end from C to D.

Wrongly Directed Energy

More men have gone astray on the simple question of the power of the lever than on any other subject in mechanics. The writer has known instances where men knew the principles involved in the lever, who would still insist on trying to work out mechanical devices in which pulleys and gearing were involved, without seeming to understand that those mechanical devices are absolutely the same in principle.

This will be made plain by a few illustrations. In Fig. 3, A is a pulley four times larger, diametrically, than B, and C is the pivot on which they turn. The pulleys are, of course, secured to each other. In this case we have the two weights, one of four pounds on the belt, which is on the small pulley (B), and a one-pound weight on the belt from the large pulley (A).

Fig 3 - The Pulley

The Lever and the Pulley

If we should substitute a lever (D) for the pulleys, the similarity to the lever (Fig. 2) would be apparent at once. The pivot (C) in this case would act the same as the pivot (C) in the lever illustration.

In the same manner, and for like reasons, the wedge, the screw and the incline plane, are different structural applications of the principles set forth in the lever.

Whenever two gears are connected together, the lever principle is used, whether they are the same in size, diametrically, or not. If they are the same size then no change in power results; but instead, thereof, a change takes place in the direction of the motion.

Fig 4 - Change of Direction

Fig 5 - Change of Direction

When one end of the lever (A) goes down, the other end goes up, as shown in Fig. 4; and in Fig. 5, when the shaft (C) of one wheel turns in one direction, the shaft of the other wheel turns in the opposite direction.

It is plain that a gear, like a lever, may change direction as well as increase or decrease power. It is the thorough knowledge of these facts, and their application, which enables man to make the wonderful machinery we see on every hand.